此内容仅用于个人学习和研究
Pearson相关用于检验两个数值变量的相关性,应用条件为两变量均符合正态分布,否则需要采用Spearman相关。除此之外,Spearman相关还可以用于检验两个等级变量的相关性。
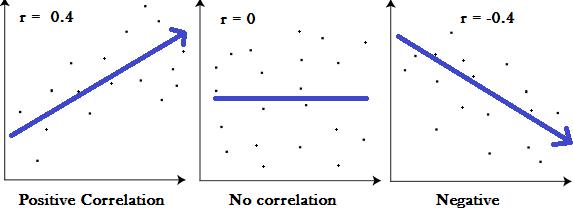
常见的变量间相关系数简介
首先简介常见的用于描述变量间相关性的系数,包括Pearson、Spearman、Kendall、Polychoric、Tetrachoric、Polyserial、(Point-)Biserial等。
Pearson相关(连续变量,数值相关)
Pearson相关系数(皮尔森相关)是使用最广泛的相关性统计量,用于测量两组连续变量之间的线性关联程度。
Pearson相关系数计算如下:
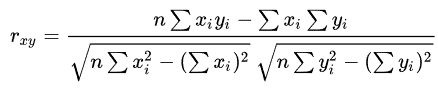
rxy,变量x和y的Pearson相关系数;
n,观测对象的数量;
xi,x的第i个观测值;
yi,y的第i个观测值。
Pearson相关系数应用于连续变量,假定两组变量均为正态分布、存在线性关系且等方差。线性关系假设两个变量之间是线性响应的,等方差假设数据在回归线上均匀分布。
Spearman秩相关(连续变量,秩相关)
Spearman秩相关系数(斯皮尔曼等级相关)是一种非参数统计量,其值与两组相关变量的具体值无关,而仅仅与其值之间的大小关系有关。Spearman秩相关依据两列成对等级的各对等级数之差进行计算,所以又称为“等级差数法”。当变量在至少是有序的尺度上测量时,它是合适的相关分析方法。
Spearman秩相关系数计算如下:
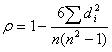
ρ,Spearman秩相关系数;
di,对应变量的秩之差,即两个变量分别排序后成对的变量位置(等级)差;
n,观测对象的数量。
Spearman秩相关同样应用于连续变量,与Pearson相关相比Spearman秩相关不要求变量的正态性和等方差假设,且对异常值的敏感度较低(该方法基于变量的排序,因此异常值的秩次通常不会有明显变化),因此适用范围通常更广。但方法较为保守,统计效能较Pearson相关系数低,容易忽略一些不太强的线性关系。
此外,Spearman秩相关要求数据必须至少是有序的,一个变量的得分必须与另一个变量单调相关(monotonically related)。
Kendall相关(分类变量,秩相关)
Kendall 相关系数则用于计算分类变量间的秩相关,用于反映分类变量相关性的指标,适用于两个分类变量均为有序分类的情况。
考虑两组变量,x和y,它们各自的观测值数量均为n,则x与y观测值可能配对的总数为n(n-1)/ 2。由于x和y为分类变量,需要首先根据类别表示的重要度人工赋值。随后考察x和y的关系对,如果xi<yi且xj<yj,或xi>yi且xj>yj,则该关系对是一致的(concordant),反正则不一致(discordant)。一致关系对数量与不一致关系对数量的差值除以总关系对数量,可得Kendall 相关系数:
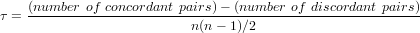
如果一致对的数量比不一致对的数量大得多,则变量是正相关的;如果一致对的数目比不一致对的数目少得多;则变量是负相关的;如果一致对的数目与不一致对的数目大致相同,则变量之间的关系很弱。
Polychoric相关(二元有序变量间的相关)
Polychoric相关(多分格相关)度量多个对象之间关于有序变量(有时称为“有序类别”数据)之间的一致性。当以列联表的形式组织数据时,两个分类自变量被排序,据此计算Polychoric相关系数。
对于2×2列联表的情况,Polychoric相关系数也称为Tetrachoric相关系数(作为Polychoric相关的一种常见类型)。通过以下对Tetrachoric相关的描述即可理解Polychoric相关的定义。
Tetrachoric相关(二元有序变量间的相关,Polychoric相关的某种常见类型)
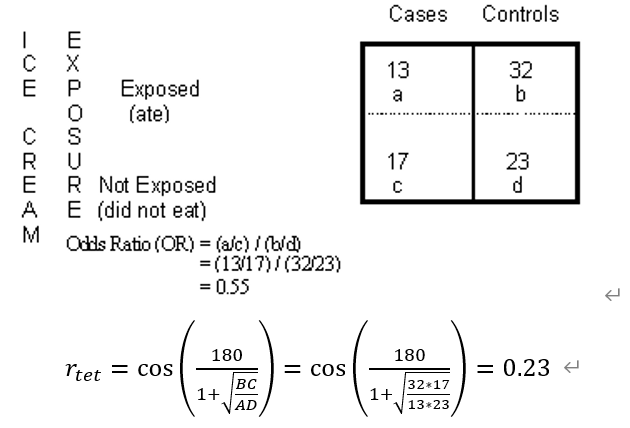
Tetrachoric相关(四分相关)是在二元正态性假设下从2×2表推断出的Pearson相关,用于测量二元数据一致性。Tetrachoric相关要求基本变量来自正态分布,并且二元数据中存在一个潜在的连续梯度,即观测值的特征应该是连续而非离散的。
首先将观察数值矩阵获得列联表,并通过下式计算:
Polyserial相关(定量变量和序数变量的相关)
Polyserial相关(多系列相关)测量的是两个连续变量之间的相关关系,它们具有二元正态分布,其中一个变量可以直接观测到(以定量数值记录),而另一个变量无法被观测(以序数值记录)。通过将可观测的连续变量分类为有限的离散有序值集,可以从可观测的有序变量获得不可观测有序变量的信息。
Biserial相关(连续变量和二元有序变量的相关,Polyserial相关的某种特例)
Biserial相关系数为Polyserial相关的一种特例,用于测量一组连续变量和一组二元变量的线性关系,二元变量是二分序数类型,具有潜在的连续性。

Y0,x=0时变量对的平均分;
Y1,x=1时变量对的平均分;
p,x=1时变量对的比例;
q,x=0时变量对的比例;
σy,总体标准偏差。
Point-Biserial相关(连续变量和二元分类变量的相关)
与Biserial相关系数相比,Point-Biserial相关系数用于测量一组连续变量和一组二元分类变量的线性关系,分类变量是无序的。
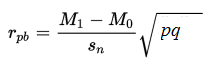
M1,二元变量组“1”对象对应的连续变量的均值;
M0,二元变量组“0”对象对应的连续变量的均值;
Sn,连续变量的标准偏差;
p,二元变量组“1”对象所占总对象的比例;
q,二元变量组“0”对象所占总对象的比例。
作为一名科研工作者,时时刻刻都在和时间赛跑。吾必须时时刻苦钻研科研,掌握现代科研的知识和技能。愿在未来,不忘初心,牢记使命。只争朝夕,不负韶华,为成为一名优秀的科研工作者而努力,努力践行科学发展观,认真学习科学发展观努力做好本职工作。
科学技术是人类社会发展的原动力。要将“做科研”培养成为一种兴趣,将实践和科研思维结合进行科学创新,才能真正推进科技进步。要如何做研究?--从实践中发现问题;运用知识储备提出问题;依赖先进的技术研究问题;最终的研究成果,要不忘初心,应用于解决实践中的问题上。
读书学习之道,看似无边无际,不知何去何从,倘若勤奋刻苦,书山自有石经,学海岂无彼岸。故不积跬步,无以至千里;不积小流,无以成江海。作为科研工作者,吾应发奋图强,刻苦学习!方能在科研方面更进一步!
此内容为个人学习笔记,外人禁止查看

